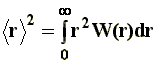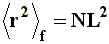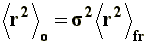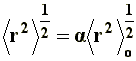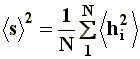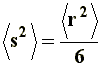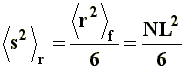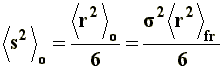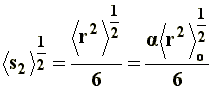|
|
|---|
The size of the macromolecule is given, in statistical terms, by the mean-square end-to-end distance, �r�2. Other authors express the root mean-square end-to-end distance, that is to say, �r2��. The magnitude �r�2 is defined according to:
|
|
[5] |
|---|
Where W is a probability distribution function.
The calculation of the mean-square end-to-end distance �r�2, varies according to the chain type, and the interactions that were taken into account.
Let's consider the simplest model of a polymer chain, i.e. an ideal polymer, consisting of a series of N segments of length L. Let's assume that the chain segments are bonded according to a linear sequence, without any restriction regarding bonding angles w and internal angles of rotation l (Figure 5), so that the atoms are separated each other at fixed distances but located in any direction. Thus, the calculation of �r�2 can be made by means of a procedure known as random flight. According to this procedure and following a mathematical reasoning (see Flory, 1971, for details) equation [5] can be re-written as follows:
|
|
[6] |
|---|
Where subscript f indicates that a random flight approximation is being considered, originating a model known as freely jointed chain.
Nevertheless, the situation is somewhat more complicated when trying to transfer the calculation of �r�2 to real macromolecules, where restrictions indeed exist, and therefore chain atoms cannot be located in any direction. Factors like solvent type, chain type, and the groups attached to the polymer backbone, do cause interactions, generating deviations from the freely jointed chain model. For this reason �r�2 is higher than that obtained by calculation of the random flight. These interactions can be divided in: short range interactions and long range interactions.
Short range interactions are related to the structural characteristics of the macromolecule, considering bond types and the interactions between segments or neighboring atoms. These factors originate steric repulsions, which limit the values of the internal angles of rotation (figure 5) since in such a case, they are not all equally probable. The magnitude of this effect is related to the size of the substituent groups. Hence the random coil will expand itself, in order to avoid such repulsions.
This model is known as unperturbed dimension, since neither interactions between non-neighboring chain segments nor solvent interactions (long range interactions, to be discussed later) are being considered. To this end, the mean-square end-to-end distance of the unperturbed dimension, �r�2o, is expressed as follows:
|
|
[7] |
|---|
Where �r�2fr represents the mean-square end-to-end distance of the free rotation chain, that is to say, under the condition that the bonding angles w (figure 5) remain fixed, independently of the presence of substituent groups. The s factor, referred to as conformation factor, is a parameter related to the impediments to rotation that real chains show, compared to that with a free chain rotation. The s factor depends on temperature and sometimes on the solvent, and offers interesting information about the conformation of a certain macromolecule and usually, it is increased in the presence of bulky groups.
Although the corrections introduced by the short range interactions offer a more approximate description of real macromolecules in dilute solutions, such interactions do not contemplate the behavior of non-neighboring chain segments, each one occupying a certain volume from which all the other segments are excluded. Such effect, known as excluded volume and its influence on the dimensions of the macromolecular chains, has been the subject of numerous studies for a long time. Its theoretical calculation has been carried out by means of statistic and the aid of computer simulation.
To this end, in order to make possible the calculation of the end-to-end distance considering the excluded volume effects, the long range interactions have been introduced, which consider both solvent interactions and interactions between atoms or non-neighboring segments. One may speculate that the long range interactions can produce a bigger chain expansion over its unperturbed dimensions, since now, due to the excluded volume effect, such conformations where two remote segments can occupy the same space at the same time should be eliminated. Hence, the end-to end distance is given by:
|
|
[8] |
|---|
Where a is the linear expansion factor, and �r�2o the end-to-end distance of the unperturbed dimension.
The value of a depends on the number of segments, the temperature, and the solvent nature. When a values are high, it is said that the solvent is thermodynamically "good". Therefore, remembering what we mentioned in previous pages, polymer-solvent interactions will be favored, making the random coil to be expanded and allowing the excluded volume effect to occur. On the contrary, when a values are low, the solvent is considered thermodynamically "poor" and the random coil will be contracted, in order to minimize the contact with its segments.
Analyzing equation [8], it can be noticed that when a = 1, a situation that can be reached with a solvent sufficiently "poor" or at low temperatures, the dimensions of the macromolecule, affected by long range interactions, matches those of the unperturbed dimension. Under such conditions, the polymer-solvent and polymer-polymer interactions are of the same magnitude, and that particular "q state", which we mentioned earlier, is reached. If such a condition was reached at a given temperature, this temperature will be considered as "q temperature" or "Flory temperature"; if it was reached in a given solvent at T = a, this solvent will be considered as a "a solvent".
By means of the preceding discussion, the relevance in the evaluation of the conformation factor s, and the linear expansion factor a, while studying the conformational properties of polymers in dilute solutions, is clearly demonstrated. While s is related to the geometry of the chains and its structural characteristics (considered by the short range interactions) a measures the magnitude of the excluded volume effect as well as polymer-solvent interactions, described through the long range interactions. The experimental determination of factors s and a, will be discussed briefly in the next section.
Radius of Gyration
In the case of branched chains, with a large number of ends, it turns out more appropriate to talk about the square-mean radius of gyration instead of the end-to-end distance, which is more applicable to linear polymers. Represented as �s�2, the radius of gyration is the square mean radius of each one of the elements of the chain measured from its center of gravity. Although �s�2 is defined according to:
|
|
[9] |
|---|
Being N the number of segments, and �hi�2 the square mean distance of i-�sim segment from the center of gravity, its value is often related to the square mean distance �r�2 through a constant, in the generic form:
|
|
[10] |
|---|
Thus, it can be noticed that the dimensions of a branched chain are smaller than those of a linear chain with the same molecular weight, or the same number of segments. This simple relation can be applied to the three situations considered in a), and if we express �s�2 in terms of equations [6[, [7], and [8] we will obtain, respectively, the value of the square-mean radius of gyration for a "freely joined chain" (equation [11]), an "unperturbed chain" (equation [12]) and a chain being affected by long range interactions (equation [13]):
|
|
[11] |
|---|
|
|
[12] |
|---|
|
|
[13] |
|---|
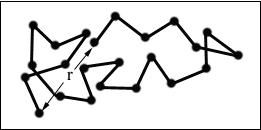
The following schematic representation of a random coil, shows the differences between the end-to-end distance (r) and radius of gyration (s).
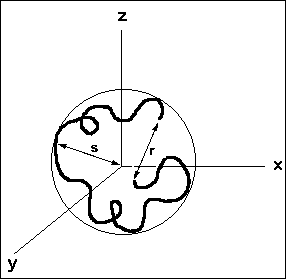
Figure 7. Redrawn from "Polymer Chemistry : An Introduction" / Malcolm P. Stevens, 2nd Ed., Oxford University Press, New York, 1990
Previous
Next
Return to Summary