Intrinsic Viscosity

Keywords
secondary interaction, hydrodynamic volume

Polymers do something weird when you dissolve them in a solvent: They make the solution viscous. You've seen this. Polymers are used as thickeners in things like shampoo and even ice cream. This thickening effect can be used to estimate a polymer's molecular weight. If you haven't read it already, this might be a good time to read the molecular weight page.

But before we talk more about molecular weights, let's first let's ask a question:

Why do polymers make solutions viscous?

For one, polymers move very slowly, or at least, they move a lot more slowly than do small molecules. It makes sense that the faster molecules in a liquid move, the more easily the liquid will flow. So when we dissolve a polymer in a solvent, their slow motion makes the whole solution more viscous.

Ok, polymers are slow. But why does the whole solution become viscous? Do polymers make the solvent molecules move more slowly, too? How?

The answer is yes. Polymers are rather pushy. It's not enough for them to move slowly themselves, but they feel they must make the solvent molecules move more slowly, too. So how and why do the polymers go about imposing their ways on the otherwise free-spirited solvent molecules?

To understand, it helps to think about a fabulous three-day holiday weekend. You're leaving town for the holiday, going on a road trip with a few of your favorite co-conspirators. You pile into your sleek, fast convertible and hit the highway, in search of adventure. But soon after merging into the fast lane you notice that your pulse is slowing a good deal. The wind that had been blowing furiously through your rebelliously wild hair has diminished to gentle summer breeze as your velocity drops. Your engine bogs down, and you have to shift down into fourth, then third, in order to keep your engine revved at these incredibly slow speeds. "How slow?" your mind wonders in frustration, as you glance at your speedometer, which now reads a paltry forty-five miles per hour!

Far ahead, in front of a long line of equally slow moving sleek convertibles, all of them in third gear, you spot a large spare tire cover which reads, "The Happy Hattson Family, Forestdale, Wisconsin". Attached to that spare tire cover is a monstrous and menacing motor home, covered in bumper stickers chronicling its many journeys to vacation heavens like Gatlinburg, Tennessee and Branson, Missouri. The motor home, filled with Happy Hattsons, is chugging away at a pace that would make a snail blush. With bitter resignation you come to accept the fact that you will be a bit late getting to your destination.

That's how it is with polymers and small molecules. The big giant motor home moving slowly in the fast lane slows down ALL the traffic on the highway. In the same way, slow moving polymers get in the way of the fast moving solvent molecules when they try to flow. So the whole solution moves more slowly, and becomes more viscous.

What's worse is that the polymer molecules do more than just block the motion of the small molecules. They also slow them down through intermolecular forces. If there are any attractive secondary interactions between the polymer and solvent molecules, the small solvent molecules can become bound to the polymer. When this happens they move with the polymer more or less, and of course, they have to move at the polymer's slow speeds. It might help to think of a small asteroid, hurtling through space, and being captured by the gravity of a large planet and becoming a satellite. In the same way, a solvent molecule coming too close to the polymer molecule will get captured and become a "satellite" of the polymer molecule.

Ok, polymers make solutions viscous. Whoopee. What does all this have to do with the business of measuring molecular weight?

This thickening effect helps you estimate molecular weight because of a simple fact: The higher the molecular weight, the more viscous the polymer solution will be. This is reasonable. When a polymer has a higher molecular weight, it has a bigger hydrodynamic volume; that is, the volume that the coiled up polymer takes up in solution. Being bigger, the polymer molecule can block more motion of the solvent molecules. It can block off more lanes of the highway, you might say. Also, the bigger a polymer is, the stronger its secondary forces are. Remember the principle of summation of molecular forces? So the higher the molecular weight, the more strongly the solvent molecules will be bound to the polymer. This enhances the slowing-down of the solvent molecules.

For most every polymer there's a definite relationship between molecular weight and viscosity. So, measure the viscosity, and we can get the molecular weight. And that's just what we're going to talk about next, measuring the viscosity of a polymer solution.

Finally...
Measuring Polymer Solution Viscosity

How do we measure the viscosity of a polymer solution? It's pretty simple, really. We just take a funny looking tube, that looks like the one in the picture, and let measure how long it takes for a given volume of the solution to flow through it.

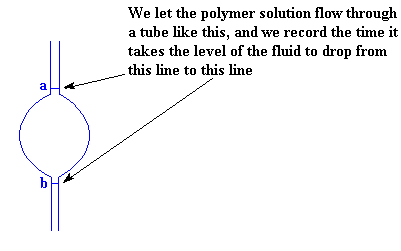
To make sure we're measuring the same volume each time, we measure the time the level the solution takes to drop from the first line (marked a in the picture) to the second line (marked b). The big bulge in the tube between the two lines is to increase the volume between the two lines. Without it, the time for the solution level to drop would be too fast to measure with just a stopwatch.

So now we know how to measure the time it takes for the solution level to drop, called an efflux time, I'll tell you some more details. We don't just do one measurement. We measure efflux times for solutions of our polymer solution at varying concentrations. We also, for comparison measure the efflux time of the pure solvent, with no polymer dissolved in it.

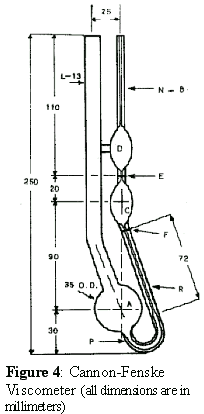And if you want to see what one type of actual viscometer looks like, take a look at the picture on the right. This type is called a Cannon-Fenske and gives pretty good data but not as good as the new kind we'll discuss below.

So what do we do with these numbers? The first thing we do is we give a name to one of them. We give a name to the efflux time of the pure solvent. We call it t0. Then we start to do some number crunching. The first thing we do is calculate the viscosity of the polymer solutions to the viscosity of the pure solvent. We do this by taking the efflux time of the polymer solution at a given concentration (we call this t) and dividing it by t0, the efflux time for the pure solvent. This gives us what we call the relative viscosity. We use the Greek letter h to denote the relative viscosity.

We're going to use the relative viscosity in minute, but first we're going to do some more number crunching with the efflux times. This time we're not going to look at the efflux time of the solution relative to that of the pure solvent. Instead, we're going to look at the difference in the efflux times of the solution and the pure solvent, relative to the efflux time of the pure solvent. Got that? We subtract the efflux time of the pure solvent, t0 from the efflux time of the solution, t. Then we take the answer we get, and divide it by t0. We call the answer the specific viscosity. Still with me? Here are the equations:

Then we crunch some more on the specific viscosity. We divide it by the concentration of the solution in question, and we get what we call the reduced viscosity:

You may have figured out that we get a different reduced viscosity at each concentration. (You have to measure lots of different concentrations in this kind of experiment.) If we were to plot reduced viscosity on the y-axis, and concentration on the x-axis, we'd get a plot that looks something like this:

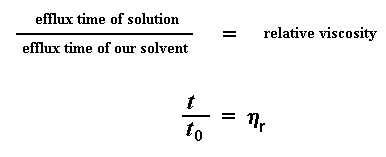
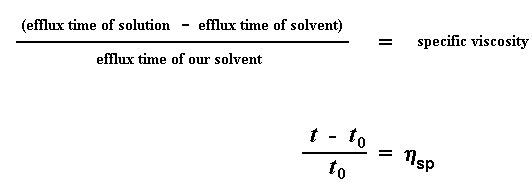
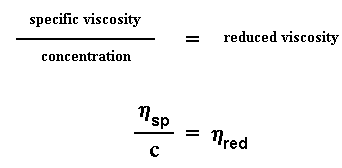
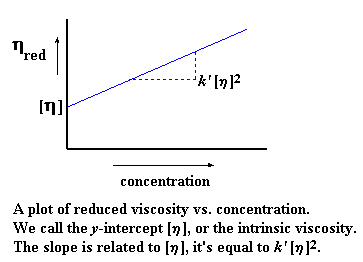
When we make this plot, we call the slope of the plot k'. We also extrapolate back to zero concentration, and call the y-intercept the intrinsic viscosity. (The intrinsic viscosity is a hypothetical construct. As viscosity varies with concentration, the intrinsic viscosity is the hypothetical viscosity at a hypothetical "zero concentration".) Think about this. If you can remember your high school algebra you might notice that this gives us an equation in slope intercept form. You know, the old y = mx + b, where is the slope of the line and b is the y-intercept:

Of course, k'[n]2 is our m, the slope of the line; and [n] is our b, the y-intercept. The intrinsic viscosity is an important number, because it's the one that will tell us the molecular weight, momentarily.

But first, you may want to take a break and go get a snack, or a drink of water, or something right now.

Are you back? Obviously, or else you wouldn't be reading this. Before we go and calculate our molecular weight from the intrinsic viscosity, I must tell you a second way to calculate the intrinsic viscosity. Remember the old relative viscosity? I told you we'd be using it, and that's just what we're going to do right now. Let's take the natural logarithm of the relative viscosity, and let's divide that number by the concentration of the solution we measured. This gives us a number we call the inherent viscosity.

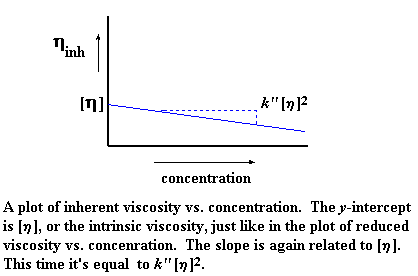
Now just like the reduced viscosity, there's a different inherent viscosity for each concentration you measure. So, we can make a plot of inherent viscosity on the y-axis, and concentration on the x-axis. Then we get a plot that looks like this:

Again, [n] is our slope intercept, but our slope this time is different, it's k'' [n]2. Yes, our plot is once again a line described by an equation in slope intercept form. Want to see it? Here it is:

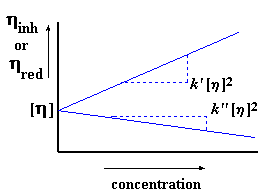
Now we usually figure up our intrinsic viscosity using both methods. If they agree, then we know we've done everything right. We usually put the plots from both methods together to get a plot that looks like this, with the two lines meeting at their common intercept:

Another way to tell if you've done everything right is that k' - k'' should equal 0.5

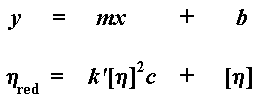
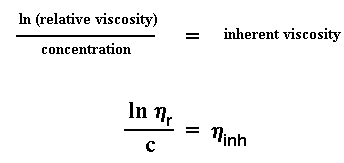
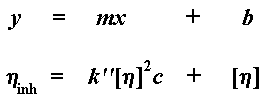
Cannon-Ubbelohde Viscometer

I bet you forgot already that I'd show you a better viscometer than the Cannon-Fenske I showed you way up above. Now's the time. The picture on the right is for that very new and improved viscometer (well, it was new back when I was learning how to do viscosity determinations, and I guess that's been quite a few years, actually, but hey, who's counting?).

"So, new and improved, you say. How so?"

Glad you asked, although I would have told you anyway. First of all, what's in the name? Ubbelohde sounds like some kind of German war machine or instrument for analyzing mine ores. It's not. In fact, I have no idea what the name means or where it came from, so if anyone out there does, let me know, please.

Here's the key advance with this simple instrument of graduate student torture. It's a "constant addition viscometer," meaning (duh!) something must be added. And that "stuff" added is solvent. You start with the highest concentration you need for your polymer solution, measure its efflux time, than add a known amount of pure solvent using an addition pipette. Let it thermally equilibrate with a little mixing, measure again. Repeat five to ten times and your done. Clean out the viscometer and measure pure solvent if you didn't do that first.

Compare that to using the Cannon-Fenske. Each measurement with it requires putting in the exact same amount of solution or pure solvent using a transfer pipette. That means you have to weigh out polymer for every concentration you need, put it in a volumetric flask, add exactly the right amount of solvent, let it dissolve till it's homogeneous. Here's the comparison: making up five to ten individual concentrations (tedious, boring, subject to errors) or making up just one (more accurate and reproducible).

And to rub salt into the wound of any student stuck with Cannon-Fenske viscometers, you can now buy an automated system that uses the Ubbelohde viscometers- a robot adds solvent for you, mixes it with a little air bubbling through, measures the efflux time and repeats as many times as you program it for. All this while you go to the cafeteria for coffee. And the robot does it all more accurately than you probably would anyway... Now back to what to do with the data.

We've done an awful lot of number crunching here, but we still haven't gotten a molecular weight. Are we ever going to?

Okay, okay, be patient. I had to go around just now because we need the intrinsic viscosity [n] to calculate molecular weight. We calculate it with a simple little equation:

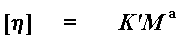
This is called the Mark-Houwink equation. M is what we call the viscosity average molecular weight (at last!) and K' and a are the Mark-Houwink constants. There is a specific set of Mark-Houwink constants for every polymer-solvent combination. So you have to know these for your particular polymer-solvent combination in order to get an accurate measure of molecular weight. This means that you can't get a good measure if you're measuring a polymer that you've just invented and there are no calculated Mark-Houwink constants available. Someone has to have made the polymer, purified it, calculated viscosities for various molecular weight fractions (or sizes), and determined the actual molecular weights using some method totally different than viscosity. The plot below shows some real data in which intrinsic viscosity was measured for several samples of the same polymer but of different molecular weight. Not a bad plot, if we do say so...

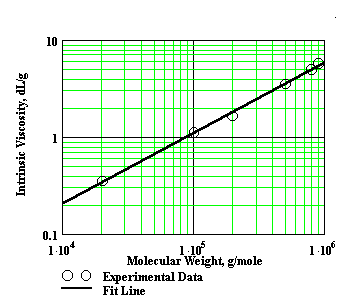
Those methods include light scattering and osmometry for starters, although size-exclusion chromatography helps a lot. But even if you don't have the Mark-Houwink constants, the intrinsic viscosity that you can easily measure can still give you a qualitative idea of whether molecular weight is high or low. The mere fact that you get an intrinsic viscosity can tell you a lot, too. Sometimes that's the only way you can tell that what you have made is, indeed, a polymer.

One last note: You have to use dilute solutions to do this kind of experiment. If the solutions are too concentrated, the polymer molecules might get close enough together to interact with each other. This causes the viscosity to increase in ways that our equations here don't describe very well, so accurate measurements can't be made. That's why this technique is called dilute solution viscometry.

Want to know some other ways of measuring molecular weight? Visit these pages!


Return to Level Five Directory
Return to Macrogalleria Directory